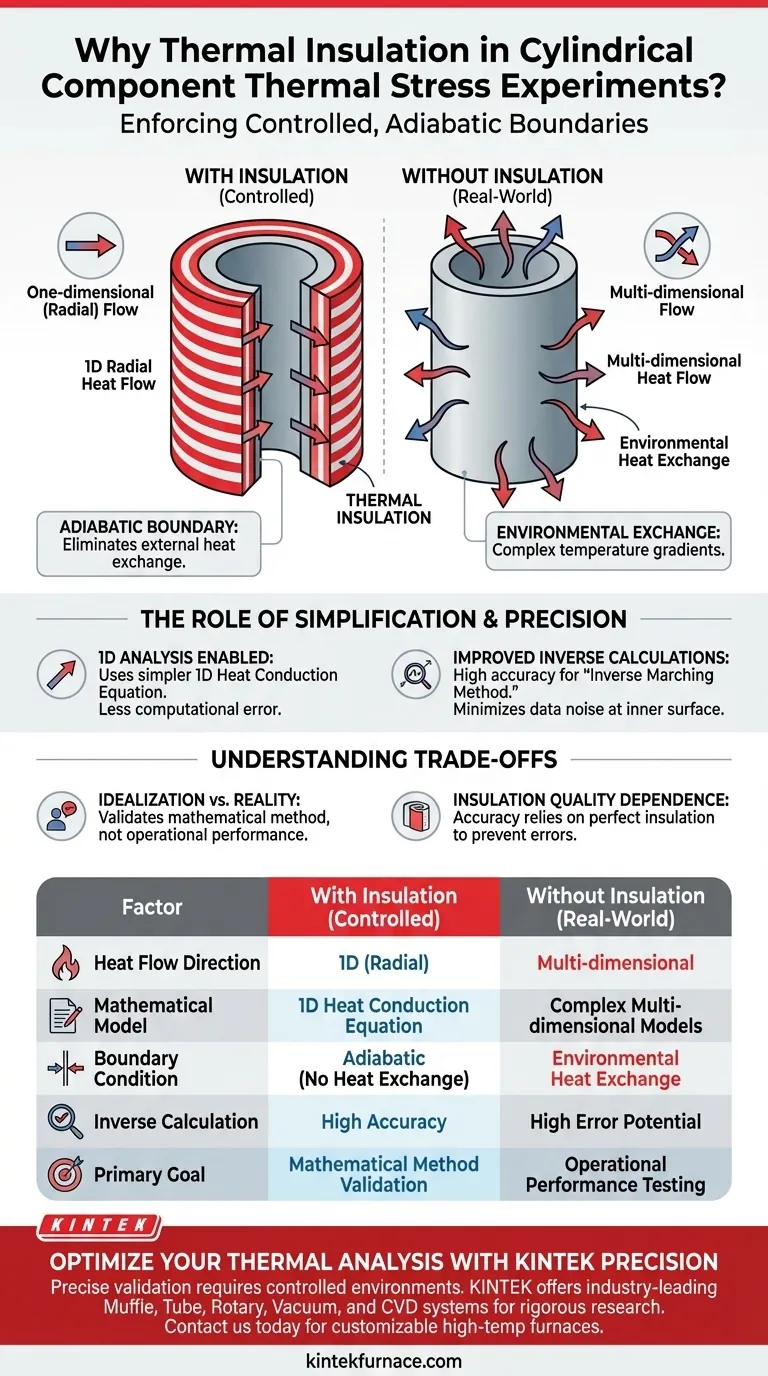
Thermal insulation is applied to enforce a controlled, adiabatic boundary condition. By isolating the outer wall, engineers eliminate external heat exchange, forcing heat transfer to occur exclusively in the radial direction. This aligns the physical reality of the experiment with the assumptions of a simplified mathematical model.
The primary purpose of insulating the outer wall is to eliminate multi-dimensional heat transfer. This ensures that the one-dimensional heat conduction equation remains valid, significantly improving the accuracy of inverse calculations used to determine stress at the inner surface.
The Role of Simplification in Validation
To validate complex thermal stress models, engineers must first control variables to ensure their mathematical equations match physical reality.
Restricting Heat Flow
Without insulation, heat would naturally escape or enter through the outer surface of a cylinder, creating complex, multi-dimensional temperature gradients.
Insulation blocks this exchange. This forces the heat to flow in only one direction: radially through the wall thickness.
Enabling One-Dimensional Analysis
When heat flow is restricted to the radial direction, the system becomes "one-dimensional."
This allows researchers to use the one-dimensional heat conduction equation. This equation is far simpler and less prone to computational error than multi-dimensional alternatives, provided the physical conditions match the math.
Improving Calculation Precision
The ultimate goal of this setup is to accurately determine what is happening at the inner surface of the component, often using data measured from the outside.
Validating the Inverse Marching Method
The text specifically refers to the "inverse marching method." This is a technique where engineers calculate temperature and stress "backwards" from a known boundary to an unknown one.
If the outer boundary allows uncontrolled heat loss, the inverse calculation loses accuracy as it "marches" inward.
Minimizing Inner Surface Error
By ensuring the outer wall is adiabatic (no heat transfer), the model minimizes noise in the data.
This results in a precise calculation of the temperature field distribution across the wall. Consequently, the derived values for temperature and thermal stress at the inner surface are significantly more accurate.
Understanding the Trade-offs
While insulation is critical for experimental validation, it introduces specific constraints that must be understood.
Idealization vs. Reality
This setup validates the mathematical method, not necessarily the operational reality of a component.
In real-world applications, pipes and cylinders often do lose heat to their surroundings. Therefore, this experimental setup is strictly for validating the accuracy of the calculation method, not for testing the component's uninsulated performance.
Dependence on Insulation Quality
The accuracy of the 1D assumption relies entirely on the quality of the insulation.
If the insulation is imperfect and allows even minor heat leakage, the 1D equation will no longer perfectly describe the physical state. This introduces errors that amplify as the calculation moves toward the inner surface.
Applying This to Your Analysis
When designing your thermal stress experiments, choose your boundary conditions based on your specific validation goals.
- If your primary focus is validating a mathematical algorithm: Use heavy insulation to enforce 1D heat flow and eliminate external variables.
- If your primary focus is operational testing: Remove the insulation to capture real-world environmental heat exchange, acknowledging that the math will require complex, multi-dimensional modeling.
By controlling the outer boundary, you transform a complex physical phenomenon into a precise, solvable mathematical problem.
Summary Table:
| Factor | With Insulation (Controlled) | Without Insulation (Real-World) |
|---|---|---|
| Heat Flow Direction | One-dimensional (Radial) | Multi-dimensional |
| Mathematical Model | 1D Heat Conduction Equation | Complex Multi-dimensional Models |
| Boundary Condition | Adiabatic (No heat exchange) | Environmental Heat Exchange |
| Inverse Calculation | High Accuracy (Inverse Marching) | High Error Potential |
| Primary Goal | Mathematical Method Validation | Operational Performance Testing |
Optimize Your Thermal Analysis with KINTEK Precision
Precise thermal stress validation starts with controlled environments and reliable heating equipment. KINTEK provides industry-leading Muffle, Tube, Rotary, Vacuum, and CVD systems, all designed to meet the rigorous demands of laboratory research and material testing.
Whether you need to enforce adiabatic boundaries for mathematical validation or simulate complex real-world heat gradients, our expert R&D team offers customizable high-temp furnaces tailored to your unique specifications.
Ready to elevate your lab's accuracy? Contact us today to discover how KINTEK's advanced thermal solutions can streamline your experimental workflows.
Visual Guide
References
- Magdalena Jaremkiewicz. Analysis of the Accuracy of the Inverse Marching Method Used to Determine Thermal Stresses in Cylindrical Pressure Components with Holes. DOI: 10.3390/en18174546
This article is also based on technical information from Kintek Furnace Knowledge Base .
Related Products
- 2200 ℃ Tungsten Vacuum Heat Treat and Sintering Furnace
- 1700℃ High Temperature Laboratory Tube Furnace with Quartz or Alumina Tube
- 1400℃ High Temperature Laboratory Tube Furnace with Quartz and Alumina Tube
- Custom Made Versatile CVD Tube Furnace Chemical Vapor Deposition CVD Equipment Machine
- 1400℃ Controlled Inert Nitrogen Atmosphere Furnace
People Also Ask
- What is the function of a vacuum sintering furnace in the SAGBD process? Optimize Magnetic Coercivity and Performance
- Why must sintering equipment maintain a high vacuum for high-entropy carbides? Ensure Phase Purity and Peak Density
- What is the purpose of setting a mid-temperature dwell stage? Eliminate Defects in Vacuum Sintering
- What is the role of a vacuum furnace in the solid-phase synthesis of TiC/Cu? Master High-Purity Material Engineering
- Why is a high-vacuum environment necessary for sintering Cu/Ti3SiC2/C/MWCNTs composites? Achieve Material Purity
