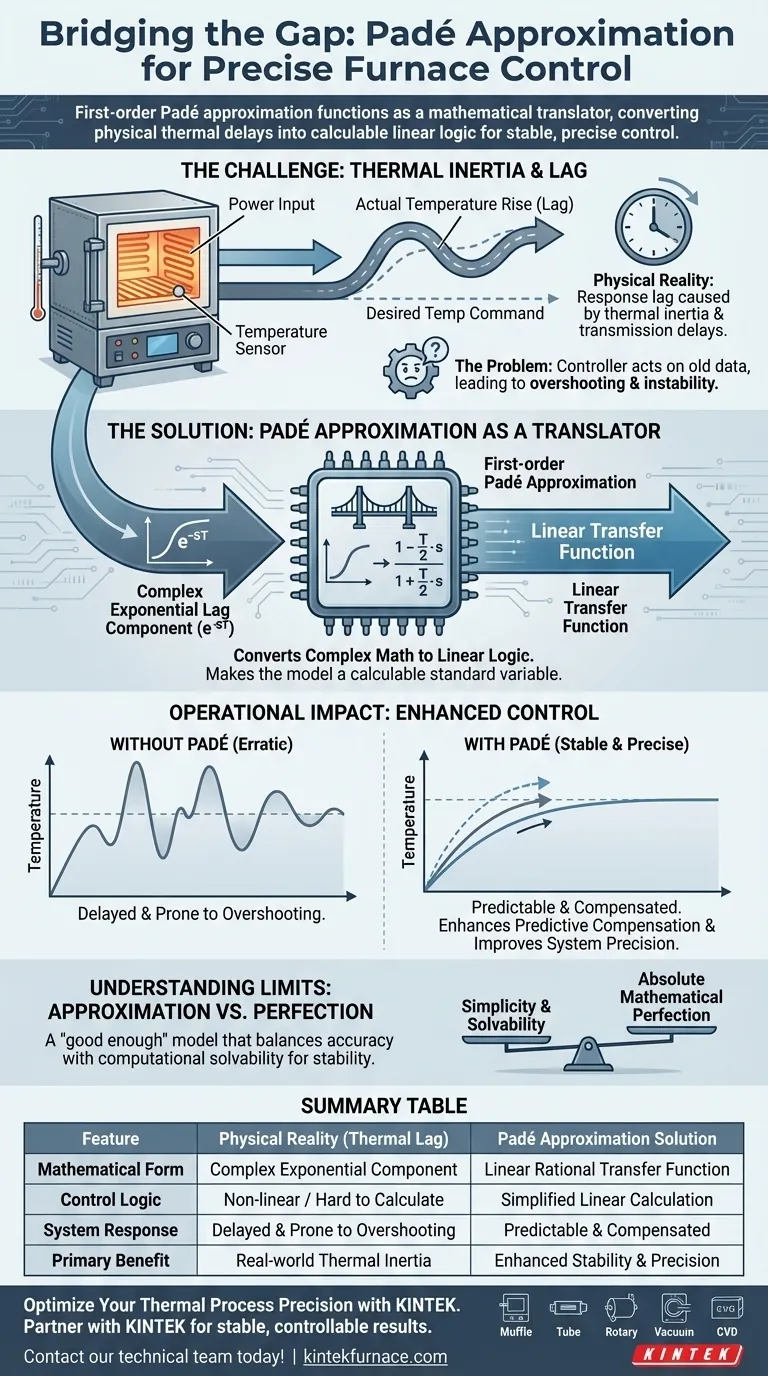
First-order Padé approximation functions as a mathematical translator that bridges the gap between physical thermal delays and control system logic. It addresses technical challenges in electric furnace regulation by converting complex exponential lag components—caused by thermal inertia and transmission delays—into a calculable linear transfer function. This transformation enables the controller to effectively compensate for response lags, ensuring the system remains stable and precise.
Industrial electric furnaces possess significant thermal inertia, creating time delays that are difficult for standard algorithms to manage. First-order Padé approximation simplifies these complex delays into a linear format, allowing the control system to predict behavior reliably and maintain precise temperature regulation.
The Challenge: Thermal Inertia and Lag
The Physical Reality of Electric Furnaces
In industrial settings, electric furnaces do not respond instantly to power changes. There is always a response lag caused by thermal inertia and transmission delays.
The Problem with Time Delays
When a controller sends a signal to increase heat, the actual temperature rise happens later. This transmission delay creates a disconnect between the command and the result.
Without proper modeling, a controller reacts to old data. This often leads to overshooting the target temperature or system instability.
How Padé Approximation Solves the Problem
Converting Complex Math to Linear Logic
Mathematically, pure time delays are represented as complex exponential lag components. These are difficult to use directly in standard linear control loop calculations.
The first-order Padé approximation solves this by converting the exponential term into a linear transfer function. It creates a mathematical rational fraction that approximates the delay.
Making the Model Calculable
Once converted, the delay becomes a manageable part of the system's equation. The control algorithm can now process the lag as a standard variable rather than a complex anomaly.
Operational Impact on Temperature Control
Enhancing Predictive Compensation
By linearizing the delay, the furnace controller can more reliably predict how the temperature will react over time. It can "see" the delay coming and adjust the power output early to compensate.
Improving System Precision and Stability
The ultimate result is a more robust system. Because the controller accounts for the thermal inertia accurately, it prevents erratic fluctuations.
This leads to enhanced precision and stability during actual operation, ensuring the furnace holds the correct temperature without constant oscillation.
Understanding the Limits of Approximation
Approximation vs. Perfection
It is important to remember that this method is an approximation, not an exact replica of the physical delay. It simplifies the infinite series of an exponential function into a finite linear ratio.
Balancing Simplicity and Accuracy
While highly effective for stabilizing standard furnace loops, it trades absolute mathematical perfection for computational solvability. It provides a model that is "good enough" to ensure stability without requiring excessive processing power.
Making the Right Choice for Your Control Strategy
When designing or tuning a temperature control model for an electric furnace, consider how this approximation aligns with your specific goals.
- If your primary focus is System Stability: Use Padé approximation to prevent oscillations caused by the delay between the heating element and the sensor.
- If your primary focus is Algorithm Simplicity: Implement this method to convert complex non-linear delay math into a standard linear function that is easy to compute.
By converting physical lag into a linear mathematical value, you transform a chaotic thermal response into a predictable, controllable process.
Summary Table:
| Feature | Physical Reality (Thermal Lag) | Padé Approximation Solution |
|---|---|---|
| Mathematical Form | Complex Exponential Component | Linear Rational Transfer Function |
| Control Logic | Non-linear / Hard to Calculate | Simplified Linear Calculation |
| System Response | Delayed & Prone to Overshooting | Predictable & Compensated |
| Primary Benefit | Real-world Thermal Inertia | Enhanced Stability & Precision |
Optimize Your Thermal Process Precision with KINTEK
Overcoming thermal inertia requires both mathematical precision and high-performance hardware. KINTEK provides industry-leading heating solutions backed by expert R&D and manufacturing. Whether you require Muffle, Tube, Rotary, Vacuum, or CVD systems, our lab high-temp furnaces are fully customizable to meet your unique temperature regulation needs.
Don't let response lags compromise your results. Partner with KINTEK to achieve the stability and control your research demands. Contact our technical team today to discuss your custom furnace requirements!
Visual Guide
References
- Serdar Ekinci, Євген Зайцев. Efficient control strategy for electric furnace temperature regulation using quadratic interpolation optimization. DOI: 10.1038/s41598-024-84085-w
This article is also based on technical information from Kintek Furnace Knowledge Base .
Related Products
- 1200℃ Controlled Inert Nitrogen Atmosphere Furnace
- 1700℃ Controlled Inert Nitrogen Atmosphere Furnace
- 1400℃ Controlled Inert Nitrogen Atmosphere Furnace
- 1200℃ Split Tube Furnace Laboratory Quartz Tube Furnace with Quartz Tube
- Spark Plasma Sintering SPS Furnace
People Also Ask
- What are the benefits of inert atmosphere heat treating? Prevent Oxidation and Preserve Material Integrity
- How does nitrogen atmosphere heat treatment improve surface strengthening? Enhance Durability and Performance
- What is nitrogen used for in a furnace? Prevent Oxidation and Control Heat Treatment Quality
- What are the applications of inert atmosphere furnaces? Essential for Metal Processing, Electronics, and Additive Manufacturing
- How does a batch type controlled atmosphere furnace operate? Master Precision Heat Treatment for Superior Materials
