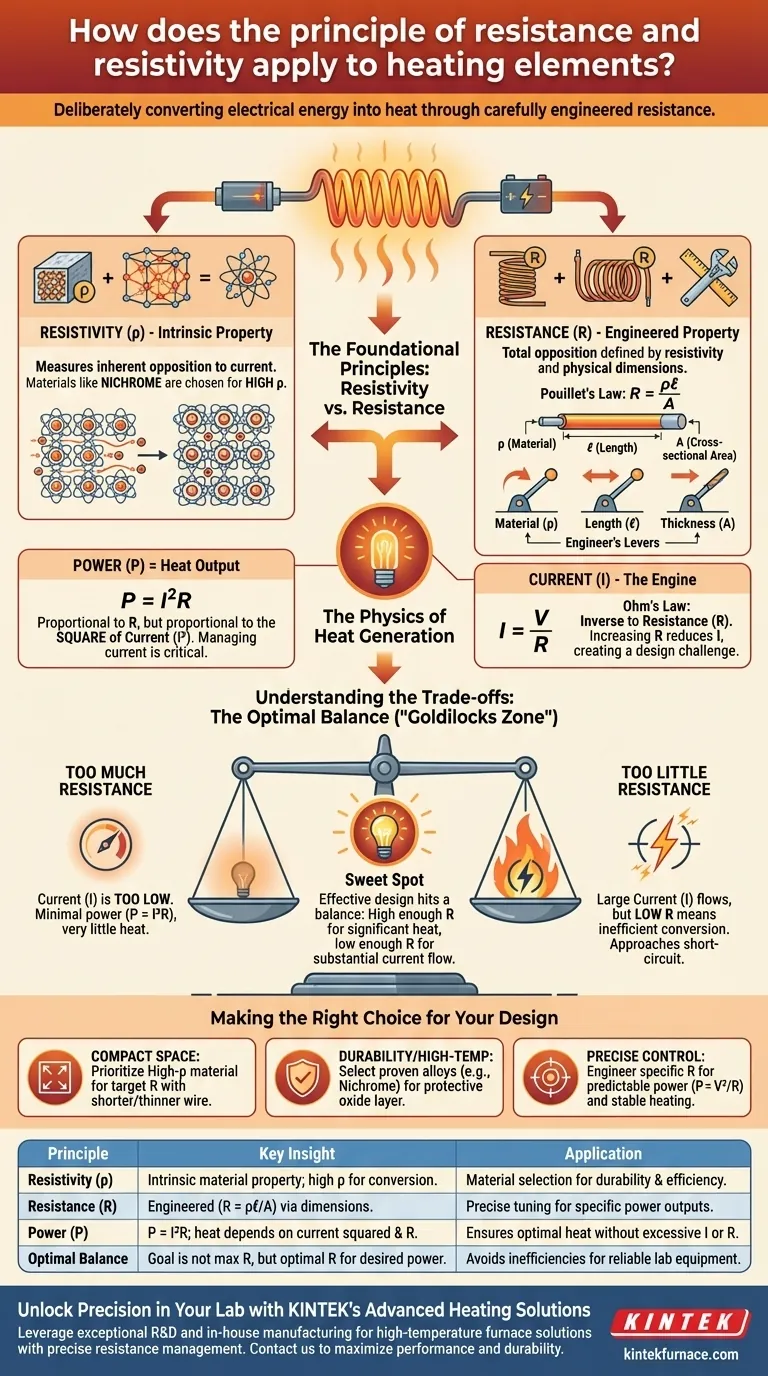
At its core, a heating element functions by deliberately converting electrical energy into heat through a material's resistance. This resistance is a carefully engineered property, determined by the material's intrinsic resistivity, its length, and its cross-sectional area, allowing for precise and efficient heat generation.
The most critical principle is not to simply maximize resistance, but to optimize it. An effective heating element strikes a perfect balance, creating enough resistance to generate heat without excessively limiting the electrical current required to produce that heat.
The Foundational Principles: Resistivity vs. Resistance
To understand how a heating element is designed, you must first distinguish between two related but distinct properties: resistivity and resistance.
What is Resistivity (ρ)?
Resistivity is an intrinsic property of a material. It measures how strongly a material inherently opposes the flow of electric current.
Materials chosen for heating elements, such as nichrome alloys, are selected specifically for their high resistivity. This ensures they can effectively convert electrical energy into thermal energy.
How Resistance (R) is Engineered
Resistance is not an intrinsic property; it is the total opposition a specific component presents to current. It is defined by the material's resistivity and its physical dimensions.
This relationship is described by Pouillet's Law: R = ρℓ/A.
- R is the total resistance.
- ρ (rho) is the material's resistivity.
- ℓ is the length of the wire.
- A is the cross-sectional area (thickness) of the wire.
This formula gives engineers three levers to pull—material (ρ), length (ℓ), and thickness (A)—to achieve a precise resistance value for a specific application.
The Physics of Heat Generation
The amount of heat produced is a function of both resistance and the current flowing through it. Understanding this interplay is key to avoiding common design misconceptions.
Power, Current, and Resistance
The heat output of an element is its power (P), measured in watts. Power is calculated as P = I²R.
This equation reveals that power is proportional to the resistance (R) but proportional to the square of the current (I). This makes managing the current a critical factor in heat generation.
The Critical Role of Current
According to Ohm's Law (I = V/R), for a fixed voltage (V), current is inversely proportional to resistance. As you increase resistance, you decrease the current.
This creates the central design challenge: increasing resistance (R) to generate heat also reduces the current (I), which is the very engine of that heat generation.
Understanding the Trade-offs: The Optimal Balance
The goal is not maximum resistance, but an optimal resistance that works with the system's voltage to produce the desired power output.
The Problem with Too Much Resistance
If an element's resistance is excessively high, it will severely impede the flow of electrons.
The resulting current (I) will be too low. Even with a high R value, the tiny I² term in the power equation (P = I²R) results in minimal power and therefore very little heat.
The Problem with Too Little Resistance
If an element's resistance is too low, it acts more like a standard conductor than a heater.
A large current will flow, but the low R value means very little electrical energy is converted into heat. This is inefficient and can approach a short-circuit condition.
Finding the "Goldilocks Zone"
Effective design involves selecting a material and geometry (length and thickness) to create a resistance that hits a "sweet spot." This value is high enough to generate significant heat but low enough to allow a substantial current to flow from the power source.
Making the Right Choice for Your Design
Your specific goal will dictate how you balance these principles.
- If your primary focus is maximizing heat in a compact space: Prioritize a high-resistivity (ρ) material, which allows you to achieve the target resistance with a shorter and thinner wire.
- If your primary focus is durability and high-temperature performance: Select a proven alloy like nichrome that forms a stable, protective oxide layer, preventing it from burning out quickly.
- If your primary focus is precise temperature control: Engineer the element's resistance (R) to be highly specific, as this ensures a predictable power output (P = V²/R) and stable, repeatable heating.
By mastering the interplay between material, geometry, and current, you can engineer heating elements that are not just hot, but also efficient, reliable, and perfectly suited to their task.
Summary Table:
| Principle | Key Insight | Application in Heating Elements |
|---|---|---|
| Resistivity (ρ) | Intrinsic material property; high ρ materials like nichrome are chosen for effective heat conversion. | Determines material selection for durability and efficiency in high-temperature environments. |
| Resistance (R) | Engineered via Pouillet's Law (R = ρℓ/A); depends on material, length, and cross-sectional area. | Allows precise tuning for specific power outputs and heat generation in lab furnaces. |
| Power (P) | Calculated as P = I²R; heat output depends on current squared and resistance. | Ensures optimal heat generation without excessive current or resistance, balancing efficiency. |
| Optimal Balance | Goal is not max resistance but optimal R to allow sufficient current flow for desired power. | Avoids inefficiencies from too high or low resistance, crucial for reliable lab equipment. |
Unlock Precision in Your Lab with KINTEK's Advanced Heating Solutions
Struggling to achieve optimal heat control in your experiments? At KINTEK, we leverage exceptional R&D and in-house manufacturing to provide high-temperature furnace solutions tailored to your unique needs. Our product line—including Muffle, Tube, Rotary Furnaces, Vacuum & Atmosphere Furnaces, and CVD/PECVD Systems—is designed with deep customization capabilities to ensure precise resistance and resistivity management for efficient, reliable heating. Whether you're in materials science, research, or industrial testing, our expertise helps you maximize performance and durability. Don't let heating challenges slow you down—contact us today to discuss how we can enhance your laboratory's capabilities!
Visual Guide
Related Products
- Laboratory Muffle Oven Furnace with Bottom Lifting
- 1400℃ Muffle Oven Furnace for Laboratory
- 1700℃ High Temperature Muffle Oven Furnace for Laboratory
- 1800℃ High Temperature Muffle Oven Furnace for Laboratory
- Multi Zone Laboratory Quartz Tube Furnace Tubular Furnace
People Also Ask
- What is the key role of a muffle furnace in the pretreatment of boron sludge and szaibelyite? Unlock Higher Process Efficiency
- How do you maintain a muffle furnace? Ensure Longevity and Safety with Proven Tips
- What metals cannot be heated by induction? Understanding Material Suitability for Efficient Heating
- How do I choose a muffle furnace? A Guide to Matching the Right Furnace to Your Process
- What is preventive maintenance on a furnace? A Proactive Strategy for Peak Performance
