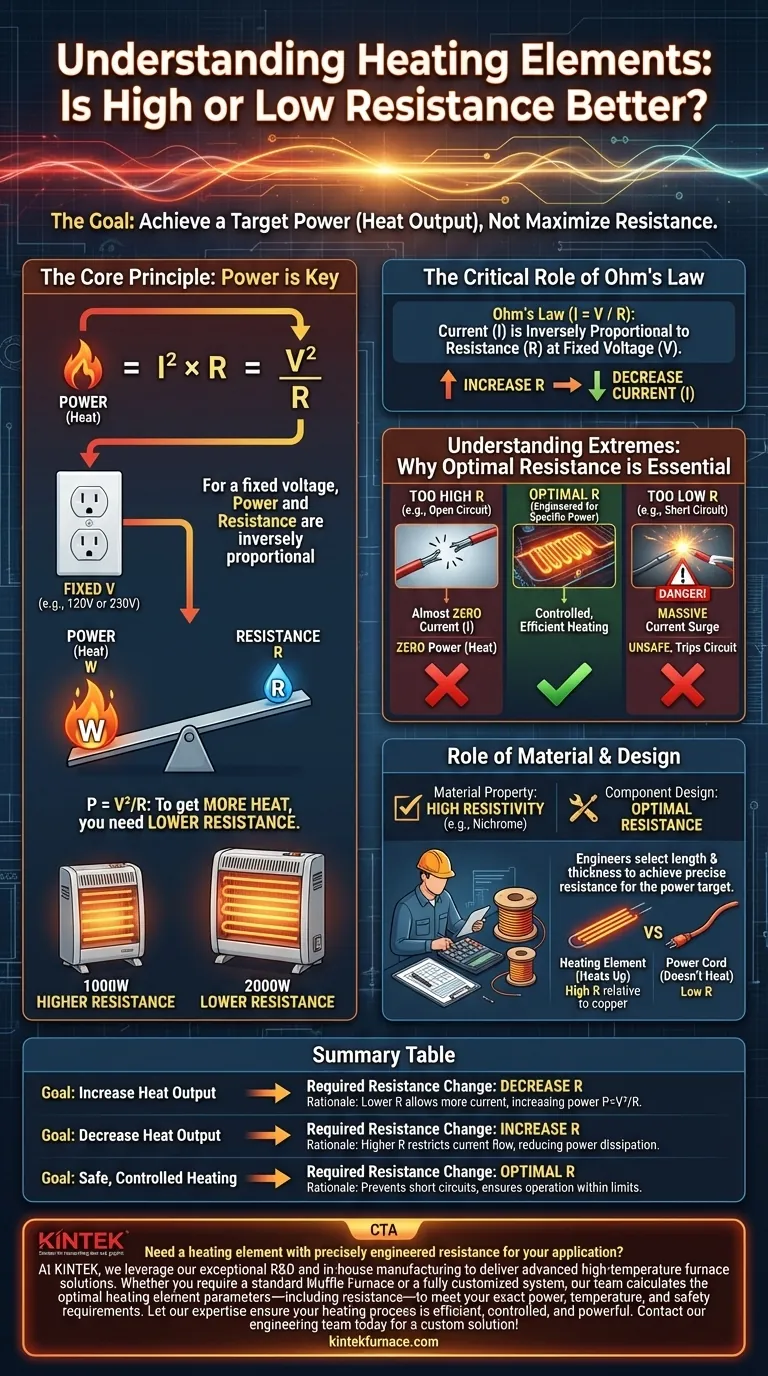
To be effective, a heating element must have a resistance that is specifically optimized for its intended voltage and desired power output. It is a common misconception that the resistance should be as high as possible. In reality, for a fixed voltage supply like a wall outlet, a more powerful heating element will actually have a lower resistance to allow more current to flow, thereby generating more heat.
The goal is not to maximize resistance, but to achieve a target power (heat) output. For a fixed voltage, power is inversely proportional to resistance (P = V²/R). Therefore, to get more heat, you need lower resistance.
The Core Principle: It's About Power, Not Just Resistance
The effectiveness of a heating element is measured in watts (W), a unit of power. Generating more heat means generating more watts. This is where the interplay between voltage, current, and resistance becomes critical.
How Heat is Actually Generated
Heat is the result of power dissipated by the element as electrical current flows through it. The power (P) is a function of both the current (I) and the resistance (R), defined by the formula P = I²R.
This formula can be misleading on its own. It suggests that increasing either current or resistance will increase power. However, these two variables are not independent.
The Critical Role of Ohm's Law
For a standard appliance, the voltage (V) from the wall outlet is a fixed value (e.g., 120V or 230V). Ohm's Law (I = V/R) states that current is inversely proportional to resistance.
This is the key insight: as you increase the resistance of the element, you simultaneously decrease the amount of current that can flow through it at a fixed voltage.
Finding the Optimal Resistance
If we substitute Ohm's Law into the power equation, we get the most useful formula for this case: P = V²/R.
This relationship makes the concept clear. Since voltage (V) is constant, power (P) is inversely proportional to resistance (R).
- To increase heat output (higher P), you must decrease R.
- To decrease heat output (lower P), you must increase R.
This is why a 2000W heater has a lower resistance than a 1000W heater designed for the same voltage supply. The 2000W model needs to draw more current to produce more power, and the only way to do that is by having a lower resistance.
Understanding the Extremes
Considering the extremes clarifies why a balanced, optimal resistance is necessary.
The Problem with "Too High" Resistance
An extremely high resistance approaches that of an insulator or an open circuit (like an air gap). According to Ohm's Law, this would choke the current down to almost zero (I = V/R).
With virtually no current flowing, the power dissipated as heat also drops to zero (P = I²R). The element simply won't heat up.
The Problem with "Too Low" Resistance
An extremely low resistance approaches a short circuit. According to Ohm's Law, this would cause a massive, uncontrolled surge of current to flow.
While this generates a tremendous amount of heat very quickly, it will immediately trip a circuit breaker or blow a fuse. It is an unsafe and unstable condition that cannot be used for controlled heating.
The Role of Material and Design
It's also crucial to distinguish between the property of a material and the final resistance of a component.
High Resistivity vs. Optimal Resistance
Heating elements are made from materials like Nichrome wire, which have a high resistivity. This is an intrinsic property meaning the material is inherently worse at conducting electricity than, for example, the copper in your home's wiring.
This high resistivity is desirable because it allows engineers to create a component with a specific, stable resistance in a compact form.
Designing for a Target Resistance
Engineers carefully choose the length and thickness of the high-resistivity wire to achieve the final, optimal resistance needed for the product.
The element's resistance is therefore "high" relative to the copper wires feeding it (which is why the element heats up and the cord doesn't), but it is precisely "low" enough to draw the exact amount of current needed to produce its rated power.
How to Apply This to Your Goal
Your goal determines the ideal resistance. The key is to stop thinking about "high" or "low" in absolute terms and start thinking about the target power you need to achieve at a given voltage.
- If your primary focus is maximum heat output: You must select an element with a lower resistance to draw more current from a fixed voltage source.
- If you are adapting a design for a lower voltage system (e.g., from 230V to 120V): You must significantly decrease the element's resistance to draw enough current to achieve the same power output.
- If your primary focus is safe, controlled heating: You need an element with a resistance carefully calculated to produce the desired watts without exceeding the amperage limits of the circuit.
Ultimately, an effective heating element is an exercise in precision engineering, where resistance is the specific tool used to hit an exact power target.
Summary Table:
| Goal | Required Resistance Change (at Fixed Voltage) | Rationale |
|---|---|---|
| Increase Heat Output | Decrease Resistance | Lower R allows more current (I) to flow, increasing power (P=V²/R). |
| Decrease Heat Output | Increase Resistance | Higher R restricts current flow, reducing power dissipation. |
| Safe, Controlled Heating | Optimal, Calculated Resistance | Prevents short circuits and ensures stable operation within circuit limits. |
Need a heating element with precisely engineered resistance for your application?
At KINTEK, we leverage our exceptional R&D and in-house manufacturing to deliver advanced high-temperature furnace solutions. Whether you require a standard Muffle Furnace or a fully customized Tube, Rotary, Vacuum, or CVD/PECVD system, our team calculates the optimal heating element parameters—including resistance—to meet your exact power, temperature, and safety requirements.
Let our expertise ensure your heating process is efficient, controlled, and powerful. Contact our engineering team today for a custom solution!
Visual Guide
Related Products
- Silicon Carbide SiC Thermal Heating Elements for Electric Furnace
- Laboratory Muffle Oven Furnace with Bottom Lifting
- 1700℃ High Temperature Muffle Oven Furnace for Laboratory
- 1800℃ High Temperature Muffle Oven Furnace for Laboratory
- Vacuum Heat Treat Furnace with Ceramic Fiber Liner
People Also Ask
- What parameters does the IEC standard specify for heating elements? Ensure Safety and Performance
- What are the operational characteristics of SiC heating elements? Maximize High-Temp Performance and Efficiency
- What types of heating elements are commonly used in drop tube furnaces? Find the Right Element for Your Temperature Needs
- What is silicon carbide used for in heating applications? Discover Its High-Temperature Durability
- What is the difference between SiC and MoSi2? Choose the Right High-Temp Heating Element
